このエントリはただの集団 Advent Calendar 2018の13日目です。 カレンダーの折返し地点です!
データアナリストにとっての悩みのひとつである、アドホックな分析における表結合。
データソースの異なる複数システムからダンプされたデータや様々なオープンデータ、表計算ファイルなどに対して、キーとなるカラムの書式、型が異なる場合、その表を結合するためには、分析の事前処理として、その変換の作業を行わなければなりません。
E.Zhuらは "Auto-join: Joining tables by leveraging transformations." (E.Zhu, Y.He, and S.Chaudhuri, 2017) のなかで、この変換処理を自動的に構築し、与えられた2つの表に対して等結合を行うAuto-Joinという仕組みを提案しました。
Auto-Joinのアルゴリズムは、大規模なデータに対しても効率的に適用され、高い確率で正確な結合が可能であることを実験で評価しています。
ここでは、同論文を解説しながら、PythonでAuto-Joinの実装を進めていきます。
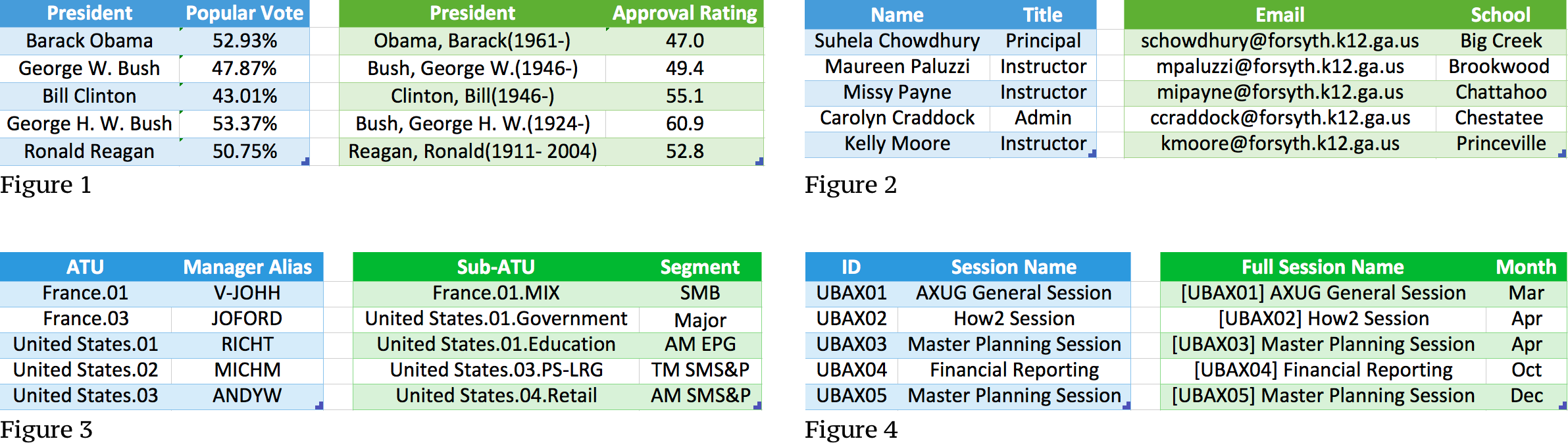
Figure 1:
- (left): US presidents and popular votes.
- (right): US presidents and job approval rating. The right table uses last-name, comma, first-name, with (year-of-birth and yearof-death).
Figure 2:
- (left): Name and job titles in school.
- (right):Email and school districts. Email from the right table can be generated from name in the left by concatenating firstinitials, last-names, and ’@forsynth.k12.ga.us’.
Figure 3:
- (left): ATU name (for area team unit).
- (right): Sub-ATU names organized under ATU.
Figure 4:
- (left): ID and session name in separate fields.
- (right): Concatenated full session name.
Source of Figures:
E. Zhu, Y. He, and S. Chaudhuri. Auto-join: Joining tables by leveraging transformations. PVLDB, 10(10):1034-1045, 2017.
Equi-Joinの限界¶
Auto-Joinが解決したい問題は何なのか。データを見ると理解が早いですね。異なるソースのデータを扱う場合 Figure 1 のように、表結合しようにも、フォーマットが異なることが多々あります。
データウェアハウスなどは、こうした問題が起こらないように、事前にETLを通じてデータクレンジングや前処理を行うですが、アドホックなデータ分析では、こういった前処理に多大な時間がかかってしまいます。
Figure 1:
- 左:
GivenName [M. [M. ]]FamilyName - 右:
Familyname, Firstname[ M. M.](yyyy-[yyyy])
このフォーマットの違いを修正する構文的変換を自動的に見つけることがこの論文のテーマです。
比較対象の先行研究として、fuzzy join という方法が挙げられており、これはトークン分割、距離関数、しきい値の組み合わせを元に、キーの組み合わせを探索するもののようです。しかし、この方法はあらゆるデータの型に合わせるにはあまりにも計算量が大きく、またその値を決めることはとても難しいと考えられます。
例えば、単語でトークン分割をする場合、
Figure 1 の最後の行
Ronald ReaganReagan, Ronald(1911-2004)
この組のJaccard距離(類似度)は$0.66$となるため、しきい値は少なくともこれ以上大きな値にならなければなりません。
$$1.0-\frac{\left|v_s\cap v_t\right|}{\left|v_s\cup v_t\right|}=1.0-\frac{\left|\{Reagan\}\right|}{\left|\{Ronald, Regan, Ronald(1911-2004)\}\right|}=1.0-\frac{1}{3}=0.66$$
しかし、しきい値を$0.66$とした場合、
George W. BushBush, George H. W.(1924-)
この組の類似度は$0.4$となり、これは正しい結果になりません。
$$1.0-\frac{\left|v_s\cap v_t\right|}{\left|v_s\cup v_t\right|}=1.0-\frac{\left|\{George,W,Bush\}\right|}{\left|\{George,W,Bush,H,(1924-)\}\right|}=1.0-\frac{3}{5}=0.4$$
しきい値に基づいた決定境界では常に正しくキーの組合せを見つけることが難しいことがわかります。
いかにして問題をとくか¶
では、この問題にどのように取り組むべきか。文字の変換を行う手順を具体的に考えてみます。
Example 1.
Figure 1の最初の行 $\{[Obama, Barack(1961-)], [47.0]\}$ を例に、どのように変換を行うかを考えてみましょう。
# 1. Input row X with two elements:
# ('Obama, Barack(1961)', [47.0])
X = ('Obama, Barack(1961)', [47.0])
# 2. Take the first item X[0], Split by "(", produce Y:
# ['Obama, Barack', '1961)']
Y = X[0].split('(')
# 3. Take the first item Y[0], Split by ",", produce Z:
# ['Obama', ' Barack']
Z = Y[0].split(',')
# 4. Takes Substring [1:] from Z[1], produce T:
# 'Barack'
T = Z[1][1:]
# 5. Concat T, a constant string " " and Z[0],
"Produced value: [%s]" % (' '.join([T, Z[0]]))
上述の例のように、分割、連結、文字切出し、などの操作を加えることで、キーを変換する必要があります。 この問題を定義すると次のようになります。
Definition 1. Transformation Join Problem: Given two tables $T_s, T_t,$ and a predefined set of operators $\Omega$, find a transformation $P=o_1\cdot o_2\cdot o_3\cdot ...o_n$, using operators $o_i \in \Omega$, such that $P(T_s)$ can equi-join with key columns of $T_t$.
$P(T_s)$の操作を行うことで、$T_t$のキー列と結合できるような列を作る$P$を発見することがこの問題の定義です。 $\Omega$は次のような操作関数の集合です。$\Omega$は要件に応じて操作を追加し拡張することも可能です。
$$\Omega = \{Split, Concat, Substring, Constant, SelectK\}$$
ただしこの問題は、1:1 join (key:key)もしくはN:1 join (foreign-key:key)を扱うものとします。
この問題では、ソースとなる$T_s$と、ターゲットとなる$T_t$のテーブルがそれぞれ存在しますが、 はじめは、どちらが、どちらであるかはわかりません。そのため、両方向から操作を行うことで、適切な方向を見つけます。
Solution Overview.¶
Step1: Find Joinable Row Pairs.¶
この問題を解く上で、$T_s$と$T_t$それぞれの値の組合せに対して計算量は二次的に増加してしまいます。 そこで、まずは一意な$q$-gramを使って行同士の関係性を見つけるというやり方で、行の組合せをを推測し計算を効率化する手順を踏みます。
Step2: Learn Transformation.¶
前の手順で得られた行の組合せを基に、$T_s$を$T_t$のキー列の型へ変換する操作を学習します。
先に見た、 Example 1 のように、最も単純な変換操作を、異なる複数の行の組から繰り返しの学習を行います。
Step3: Constrained Fuzzy Join.¶
不揃いで、汚いデータを扱う際に、そうした汚れを許容するための手順です。
たとえば、 Figure 2 の右表2行目 mipayne@forsyth.k12.ga.us は他の行のルールに従うならば、 mpayne@forsyth.k12.ga.us でなければなりません。
こうしたデータでの結合のカバレッジを広げるために、ここではfuzzy joinの自動調節をおこないます。
Table 1: Notations used for analyzing q-gram matches
また、$q$-gram 一致の分析をするにあたって、記法も整理しておきます。
| Symbol | Description |
|---|---|
| $T_s, T_t$ | $T_s$ is the source table, $T_t$ is the target table. |
| $R_s, R_t$ | A row in $T_s$ and $T_t$, respectively |
| $C_s, C_t$ | A column in $T_s$ and $T_t$, respectively |
| $Q_q(v)$ | The q-grams of string value $v$ |
| $Q_q(C_s)$ | The multi-set of all q-grams of distinct values in Cs |
| $Q_q(C_t)$ | The multi-set of all q-grams of distinct values in Ct |
$Q_q(C)$は与えられた文字列に対して、指定された$q$で分割された$q$-gramの部分列集合を返します。
example:
$$Q_5(Database)=\{Datab,ataba,tabas,abase\}$$
1-to-1 q-Gram Match¶
$T_s$と$T_t$の両方に、一意の$q$-gramが存在するとしたら、その行はまず間違いなくjoinable rowであることは直感的にわかります。(Figure 1では、Barackという$q$-gramはこれに当たりますね)
ここで次のように、$p_q(k)$という式を定義してみましょう。 $k$が大きい、つまり、その$q$-gramの発生頻度が低い場合、その確率は低くなるので、感覚的に理解ができます。
$$p_q(k)=\frac {\frac{1}{k^{s_q}}} {\sum_{z=1}^{N}\frac{1}{z^{s_q}}}$$
- $p_q(k)$ : the probability mass function for a $q$-gram whose frequency ranks at position k among all $q$-grams
- ある$q$-gram がすべての$q$-gram中の、$k$番目になる確率
- $k$ : rank of a
q-gramby frequency (頻出度ランク) - $N$ : total number of
g-gram - $s_q$ : constant for a given $q$
この$P_q(k)$式をもとに、次の命題を立てましょう。
Proposition 1. Given two columns $C_s$ and $C_t$ from tables $T_s$ and $T_t$ respectively, each with $N$ $q$-grams from an alphabet of size $\left|\Sigma\right|$ that follow the power-law distribution above. The probability that a $q$-gram appears exactly once in both $C_s$ and $C_t$ by chance is bounded from above by the following.
$$\sum_{k=1}^{|\Sigma|^q} \big( (1-p_q(k))^{N-1} \cdot p_q(k) \big)^2$$
すべての$q$-gramの数を$N$、またそれを構成するアルファベットの文字数を$\left|\Sigma\right|$とおくと、$q$-gramが$C_s$, $C_t$に一度だけ出現する確率は命題のように表すことができます。
命題の証明については、参考論文のAppendix Cを参照ください。
$N$数が増えるほど、この確率は指数関数的に小さくなります。
1-to-1 $q$-gram matchのまとめとして、1-to-1マッチが起きる条件を、次のように定義することにします。
Definition 2. Let $g$ be a $q$-gram with $g \in Q_q(v_s)$ and $g \in Q_q(v_t)$. If $F_q(g, C_s) = 1$ and $F_q(g, C_t) = 1$, then $g$ is a 1-to-1 $q$-gram match between row pair $R_s$ and $R_t$ with respect to the pair of column $C_s$ and $C_t$.
- $Q_q(C)$ : the multi-set of all the $q$-grams of distinct values in column $C$
- $F_q(g, C)$ : the number of occurences of a $q$-gram $g \in Q_q(C)$.
- あるグラム$g$のカラム$C$における出現回数
- $v_s$ : the cell value at row $R_s$ column $C_s$ in $T_s$
- $v_t$ : the cell value at row $R_t$ column $C_t$ in $T_t$
E.Zhu(2017)らの実験では、実データのベンチマークでは1-to-1 $q$-gramによる組合せは95.6%の精度となったようです。
General n-to-m q-Gram Match¶
実世界の問題では、$q$-gramの組合せが1-to-1になることは稀であるため、より現実的な場合を考えていきましょう。
Definition 3. Let $g$ be a $q$-gram with $F(g, C_s) = n \geq 1$ and $F(g, C_t) = m \geq 1$, then $g$ is a n-to-m $q$-gram match for corresponding rows with respect to the pair of column $C_s$ and $C_t$.
We use $\frac{1}{n \cdot m}$ to quantify the “goodness” of the match.
と言われているように、この問題は$n\cdot m$の最小化問題として考えることができます。
Efficient Search of q-Gram Matches¶
最後に、この一致する$q$-gramの探索を効率よく計算する方法を考えていきましょう。
一致する$q$-gramを探索する単純なアルゴリズムを考えると、次のようになります。
- すべてのセルに対して
- すべての設定可能な$q$について
- トークナイズされたそれぞれの$q$-gramについて
- テーブルのなかの、すべての値をイテレートして一致する$q$-gramを数え、これを$n$とし、
- 別のテーブルのなかのすべての値をイテレートして一致する$a$-gramを数え、これを$m$とする
これは、n-to-m matchとして表すことができますが、見るからに非効率なやり方に思えます。
まずはじめに、2つのテーブルのすべてのカラムについてsuffix array index を作成します。
対数的な計算量になるような工夫を施し、$S$はユニークなSuffixの数として計算量を$O(log S)$とすることができます。
suffix array indexの生成例を次に示します。
m = 'thagino@tadano.co.jp'
[m[c:len(m)] + '$' * c for c in range(0, len(m))]
suffix arrayを使うことで、$q$-gramの探索においてバイナリ探索を用いることで効率化が可能です。
- $g^*$: as the best prefix of all possible suffixes of $v$
- $v$の取りうるすべてのSuffixに対して、最も当てはまりのよい最強の$q$-gramを$g^*$として、この$g^*$を決めるという問題に置き換えます。
$$g^*= \underset{ \forall_g \in \operatorname{Prefixes}(u), u \in \operatorname{Suffixes}(v)} {\operatorname{arg max}} \frac{1}{nm}$$
$n=F(g,C_s)\gt0$ and $m=F(g,C_t)\gt0$は$C_s$と$C_t$それぞれに一致する数です。 このとき、$q$について、次のような命題を立てましょう。
Proposition 2. Let $g_u^q$ be a prefix of a suffix $u$ with length $q$. As the length increases by 1 and $g_u^q$ extends at the end, the $\frac{1}{nm}$ score of the longer prefix $g_u^{q+1}$ is monotonically non-increasing, or $F(g_u^{q+1},C_s) \le F(g_u^q,C_s)$ and $F(g_u^{q+1},C_t) \le F(g_u^q,C_t)$.
命題の証明については、参考論文のAppendix Cを参照ください。
Putting it together: Find Joinable Rows¶
それでは、ここまでの議論を用いて、実際に探索のアルゴリズムを構築していきましょう。
Algorithm 1
$C_s$のユニークな値$v \in C_s$について$\operatorname{OptimalQGram}$を適用します。 先の命題で定めたように、これは最適な$q$-gramを探索する問題の過程です。
$$\{g^*, score, R_s, R_t\} \leftarrow \operatorname{OptimalQGram}(v, C_t)$$
この問題は$\frac{1}{nm}$を最大化するgを見つけることが命題であり、$g^*$のときのペアとなる行とそのスコア$score=\frac{1}{nm}$である。
Suffixインデックスのすべてに対して
$$\forall_u \in \operatorname{Suffixes}(v)$$
最適な値となる$q$を
$$q^* \leftarrow \operatorname{BinarySearchQ}(u, C_t)$$
- $\operatorname{BinarySearchQ}(u,C)$ : performs the binary search of $q^*$ that finds $g_u^{q^*}$
- あるCのなかでSuffix $u$に対する最適なPrefix $g^*$となる$q^*$を返す関数
Python Implementation of Find joinable row pairs¶
では、Algorithm 1 Find joinable row pairs をPythonで実装してみましょう。
表のデータ構造として、pandas.DataFrameを使うことにする。
import pandas as pd
ts = pd.DataFrame([
('Barack Obama', '52.93%'),
('George W. Bush', '47.87%'),
('Bill Clinton', '43.01%'),
('George H. W. Bush', '53.37%'),
('Ronald Reagan', '50.75%'),
], columns=['President', 'Popular Vote'])
tt = pd.DataFrame([
('Obama, Barack(1961-)', 47.0),
('Bush, George W.(1946-)', 49.4),
('Clinton, Bill(1946-)', 55.1),
('Bush, George H. W.(1924-)', 60.9),
('Regan, Ronald(1911-2004)', 52.8)
], columns=['President', 'Approval Rating'])
それでは参照論文の疑似コードと対比して見ていきましょう。
- $\operatorname{KeyColumns}(T)$ : returns all the single columns that is part of a key column in the table $T$.
pandas.DataFrameを使うことでイテレータを利用できるため、今回はdtype = 'object'のものに絞ったDataFrameのイテレータを返すようにしました
- $\operatorname{Suffixes}(v)$ : returns all suffixes of a value $v$.
- 一致する$q$-gramを探す議論のなかで例示したように、与えられた$v$に対するすべてのsuffixをリストを返します
- $\operatorname{QueryIndex}(C,g)$ : uses a suffix array index built for the column $C$, and returns a list of rows containing $g$.
panras.Seriesを渡して与えられた$g$を含む要素を返すようにしました
- $\operatorname{SortByScore}$
- $\operatorname{MaxByScore}$ : returns the optimal row pairs with the hightest score.
- $q^*$ : leads to the highest score should results in the smallest possible non-zero number of matches in $C_t$.
- マッチ数が少なければ$\frac{1}{mn}$は大きくなる
- $r_t$ : the matching rows in $C_t$ returned by $\operatorname{QueryIndex}$
- calling $\operatorname{QueryIndex}(C_t,g_u^{q^*})$ results in $|r_t| \ge 1$, while calling $\operatorname{QueryIndex}(C_t,g_u^{q+1^*})$ results in $|r_t|=0$.
# KeyColumns(T)
def key_columns(t):
return tt.select_dtypes(include='object').iteritems()
# Suffixes(v)
def suffixes(v):
return [v[c:len(v)] for c in range(0, len(v))]
# QueryIndex(C, g)
def query_index(c, g):
return c[c.str.contains(g)]
# SortByScore
def sort_by_score(m):
return sorted(m, key=lambda t:-t[-1])
# MaxByScore
def max_by_score(m):
return sort_by_score(m)[0]
# Pairs
from itertools import product
def pairs(rs, rt):
return list(product(rs, rt))
$FindJoinableRowPairs$を実装するまえに、$BinarySearchQ$について考えていきます。 先にも説明をしましたが、$\operatorname{BinarySearchQ}(u,C)$は、あるCのなかでSuffix $u$に対する最適なPrefix $g^*$となるような最高な$q^*$を返す関数です。 下記の実装でも示すように、$h\leftarrow a+(b-a)/2$とすることで、効率的なバイナリサーチができるようになります。
# BinarySearchQ
def binary_search_q(u, ct):
"""
Parameters
----------
u : string
Suffix string.
ct : Series
A column in T_t
"""
a = 3
b = len(u) + 1
while a < b:
h = int(a + (b - a) / 2)
rt = query_index(ct, u[0:h])
# TODO implement absolute value
if rt.size > 0:
a = h + 1
else:
b = h
return a - 1
最適な$q$-gramを決めるために、セルの値$v$のすべてのSuffixに対して、$BinarySearchQ(v)$を計算し、それぞれの$q$とそのときの$\frac{1}{nm}$を求め、値が最大のものを返すような操作をします。
# OptimalQgram
def optimal_qgram(v, cs, ct):
res = []
for u in suffixes(v):
q = binary_search_q(u, ct)
if q < 3 or q > len(u):
continue
g = u[0:q]
rs = query_index(cs, g)
rt = query_index(ct, g)
score = 1/rs.size*rt.size
m = [(g, ks, kt, score) for ks, kt in pairs(rs, rt)]
res.append(max_by_score(m))
return res
ここまでで定義してきた関数を用いて、$FindJoinableRowPairs$を実装してみましょう。
結果を見やすくするために、暫定的にアウトプットをpandas.DataFrameにしています。
# FindJoinableRowPairs
"""
This function is based on
- Algorithm 1 Find joinable row pairs
- Algorithm 3 Complete pseudo code for joinable row pair
"""
def find_joinable_row_pairs(ts, tt):
"""
Parameters
----------
ts: DataFrame
T_s subject table
tt: DataFrame
T_t target table
"""
m = []
for ks, cs in ts.iteritems():
for ks, ct in key_columns(tt.columns):
m.append(cs.apply(lambda v: optimal_qgram(v, cs, ct)))
return pd.DataFrame(m).transpose()
それでは実際に、Figure 1のデータを渡して、結果を見てみましょう。
find_joinable_row_pairs(ts,tt)
$C_s$ is not needed in finding $g_u^{q^*}$とあるように、$q^*$の探索では、$T_t$のみに探索を行います。その理由としては
- $n=|r_s|>0$が常に成り立つ
when $m=|r_t|=0$, the score $\frac{1}{nm}$ becomes undefined and thus the corresponding $q$ is infeasible. Therefore, $q^*$ is only obtained at the conditions mentioned above, and is not dependent on $C_s$.
$\operatorname{BinarySearchQ}(u,C)$ performs the binary search of $q^*$ that finds $g_u^{q^*}$ in $C$.
- 最適な$q$、つまりサフィックスに対してもっとも長いプレフィックスを見つけることのできる$q$を、バイナリサーチをかけることで見つけます
- $q\lt3$のときはパフォーマンスに影響が出るため、ブレイカーを設けている
続いて、Learn Transformations についても同様に理論を理解し、Pythonでの実装を進めますが、これについては、日を追って加筆を行います。